2021年 東京都 一次・分割前期 数学の大問5(2)の解き方を見てみましょう。
大問5の問題はこちら
辺BCの長さが与えられていますが、三平方の定理も出題範囲に含まれていれば、
BC $=$ $\sqrt{\text{AB}^2+\text{AC}^2}$
で求めることができます。
↓大問5(2)の典型的な解き方です。
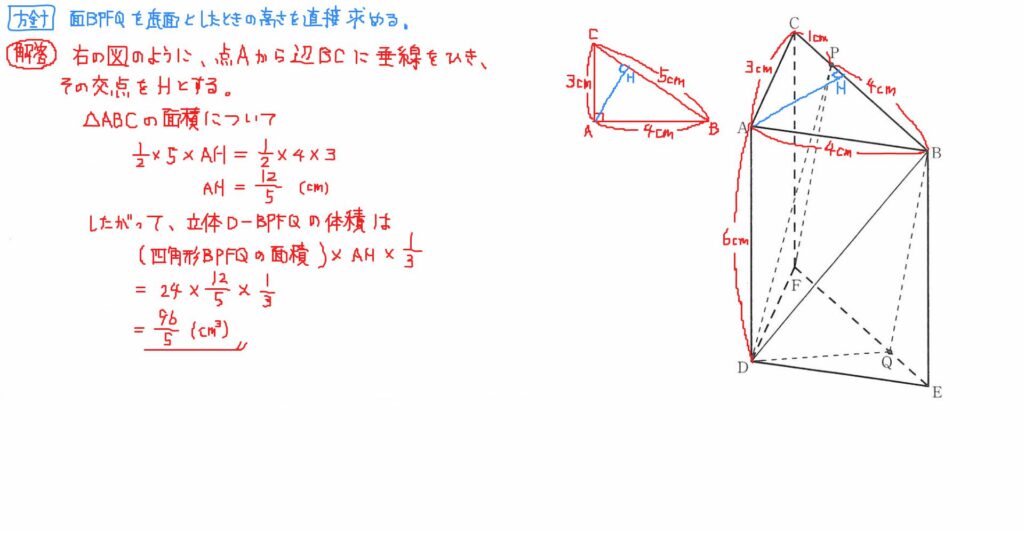
また、下の画像のように、体積比を用いて考えることもできます。
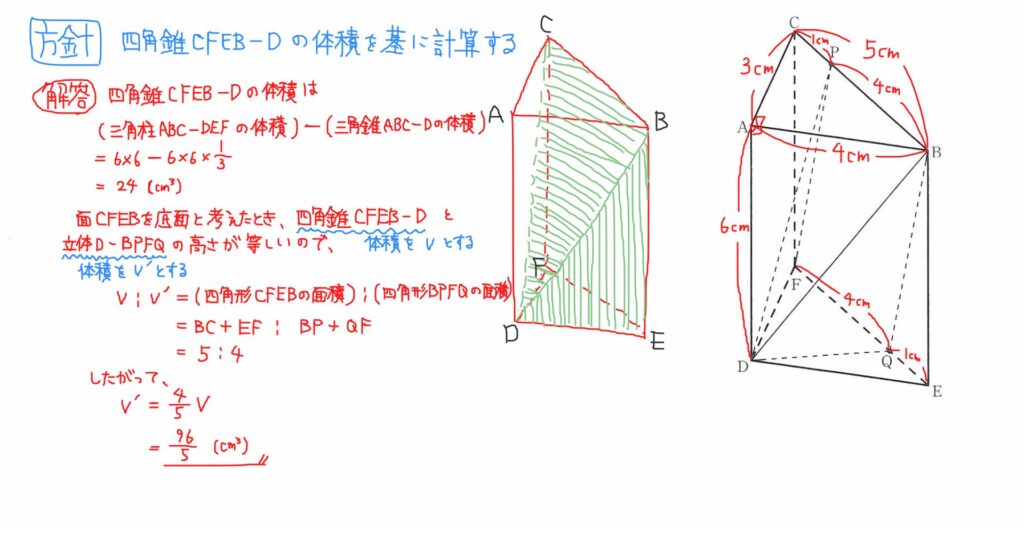
本問の問題設定においては、前者の解き方よりも計算量が多くなってしまっていますが、この解き方は最大の利点をもっています。
辺BCの長さが与えられていなくても、BP:PC が与えられていればよいのです。
実際、上の画像の $V:V’$を計算しているところで、$\text{BC}+\text{EF}:\text{BP}+\text{QF}$の部分を、線分の長さではなく線分比で置き換えても同じ結果が得られます。
つまり、中1の範囲(相似や三平方の定理は使わない)で解けるということです。
1つの問題に対して、(模範解答とは)別の解き方で解いてみることは、数学の良いトレーニングになります。
試験中に時間が余ったときにこれができれば、検算にもなるので自信をもって解答することができます。
体積をかしこく求めよう〔2021 東京都〕
2021年 東京都 一次・分割前期 数学の大問5(2)の解き方を見てみましょう。
大問5の問題はこちら
辺BCの長さが与えられていますが、三平方の定理も出題範囲に含まれていれば、
BC $=$ $\sqrt{\text{AB}^2+\text{AC}^2}$
で求めることができます。
↓大問5(2)の典型的な解き方です。
また、下の画像のように、体積比を用いて考えることもできます。
本問の問題設定においては、前者の解き方よりも計算量が多くなってしまっていますが、この解き方は最大の利点をもっています。
辺BCの長さが与えられていなくても、BP:PC が与えられていればよいのです。
実際、上の画像の $V:V’$を計算しているところで、$\text{BC}+\text{EF}:\text{BP}+\text{QF}$の部分を、線分の長さではなく線分比で置き換えても同じ結果が得られます。
つまり、中1の範囲(相似や三平方の定理は使わない)で解けるということです。
1つの問題に対して、(模範解答とは)別の解き方で解いてみることは、数学の良いトレーニングになります。
試験中に時間が余ったときにこれができれば、検算にもなるので自信をもって解答することができます。
共有: