今回は2021年に愛媛県公立高校で出題された問題の大問５の３を取り上げます。
愛媛県でも、新型コロナウイルスなどに対する配慮から出題範囲の削減は行われましたが、図形の問題には影響ありませんでした。
（三平方の定理も範囲に含まれています。）
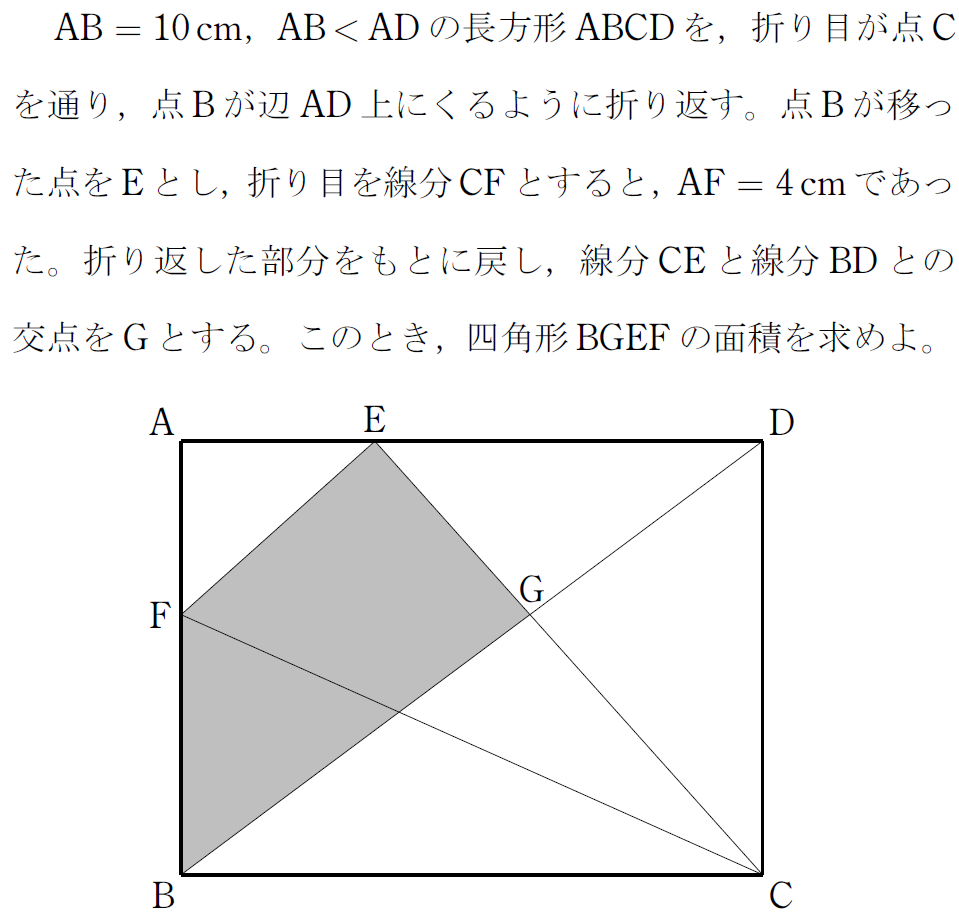2021年 愛媛県 大問５の３
長方形を折り返すだけであれば頻繁に見かけるのですが、唐突に線分BDを結んで交点Ｇをつくり、四角形BGEFを作っています。
一見すると少々面倒な計算問題ですが、解いてみると実は隠れた背景をもつ超良問であることがわかったのです。
目次〔2021 愛媛県 大問５の３のみ〕
- 普通の解き方
……まずは普通に解いてみます。
- 図形的性質を用いて解く
……超良問と称した理由がここにあります！
↓ ここまでは２つの解き方で共通しています。
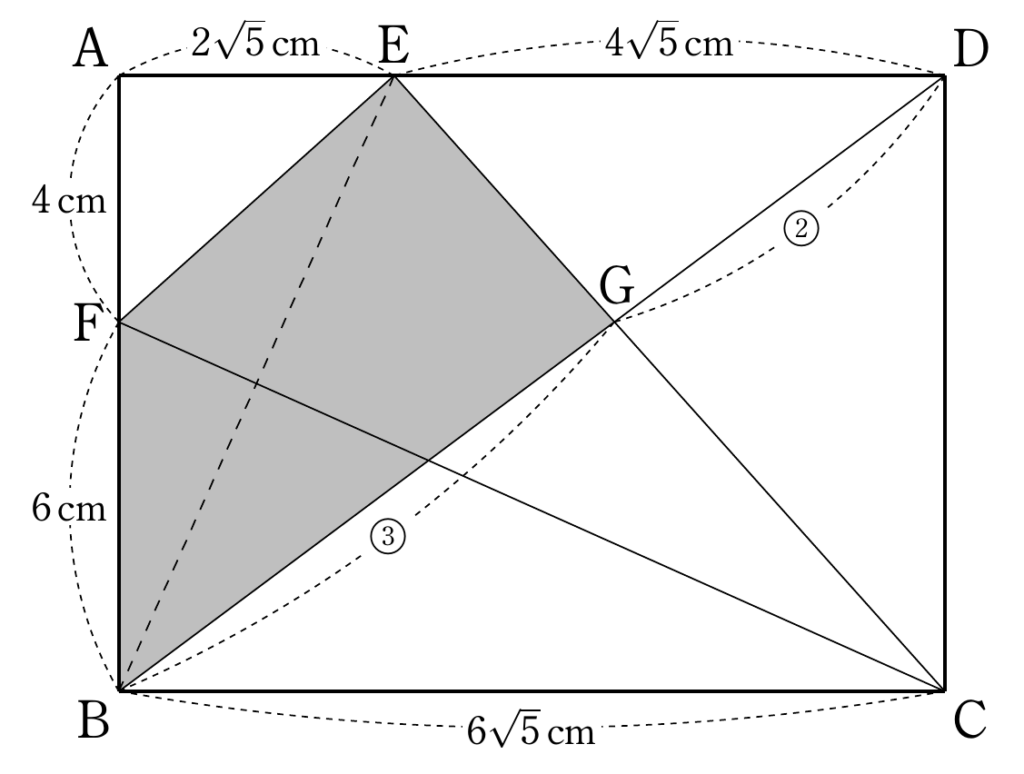
$\text{EF}=\text{BF}=6$ cmだから、△AEFにおいて三平方の定理より、
$\text{AE}=\sqrt{\text{EF}^2-\text{AF}^2}=2\sqrt{5}$ cm
△AEF∽△DCEより、
$\text{AE}:\text{DC}=\text{AF}:\text{DE}$
$2\sqrt{5}:10 = 4:\text{DE}$
$\text{DE}=4\sqrt{5}$ cm
普通の解き方
△BCG∽△DEGより、
$\text{BG}:\text{DG}=\text{BC}:\text{DE}=3:2$
よって、
△BEG $=\displaystyle{\frac35 △\text{BED}=12\sqrt{5}}\,\text{cm}^2$
また、
△BEF $=6\sqrt{5}\,\text{cm}^2 $
ゆえに、
四角形BGEF $=12\sqrt{5}+6\sqrt{5}=18\sqrt{5}\,\text{cm}^2 $
このくらいの計算問題であれば、対応できた受験生もいたかと思われます。
ただ、この $18\sqrt{5}$ という結果は、△BCF（△CEF）の面積と一致していることに着目します。
図形的性質を用いて解く
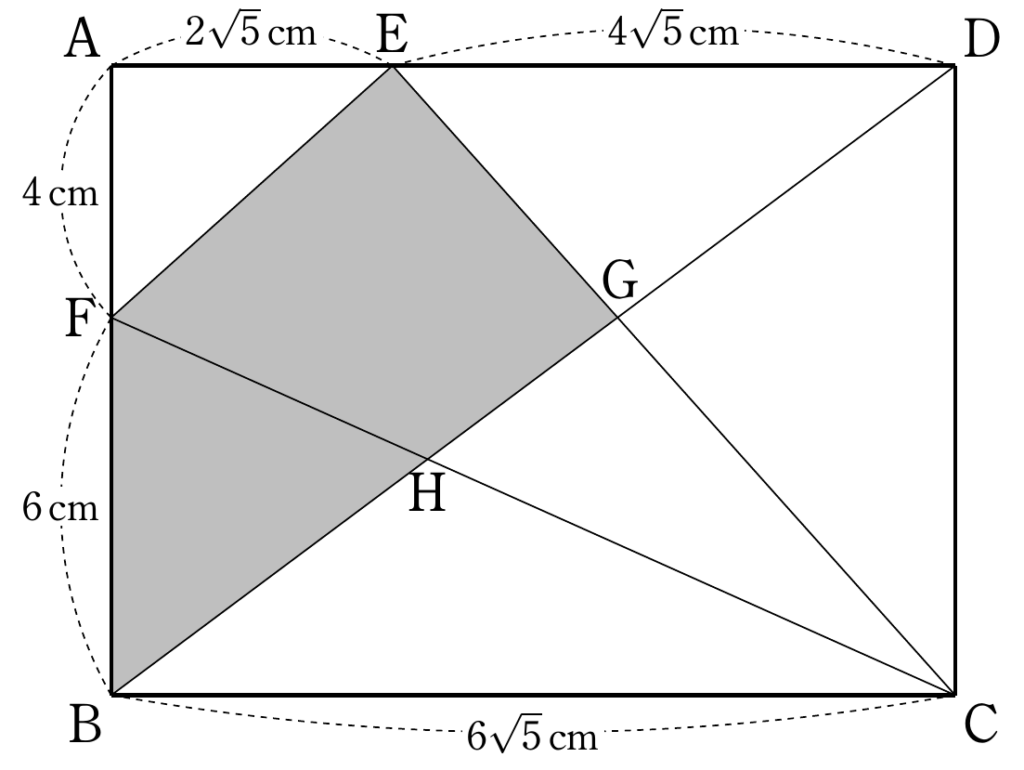
FG $/\!/$ BC であることを証明する。
$\text{AF}:\text{FB}$
$=\text{AF}:\text{FE}$ （折り返した図形の対応する辺 $\text{BF}=\text{EF}$より）
$=\text{DE}:\text{EC}$ （△AEF∽△DCEより）
$=\text{DE}:\text{BC}$ （ 折り返した図形の対応する辺 $\text{EC}=\text{BC}$より）
$=\text{DG}:\text{GB}$ （△BCG∽△DEGより）
よって、 FG $/\!/$ BC である。
BDとCFとの交点をHとすると、△BHF $=$ △CHGだから、
四角形BGEF
$=$ 四角形HGEF $+$ △BHF
$=$ 四角形HGEF $+$ △CHG
$=$ △CEF
よって、
四角形BGEF $= \displaystyle{\frac12\times 6\times 6\sqrt{5}=18\sqrt{5} \,\text{cm}^2 }$
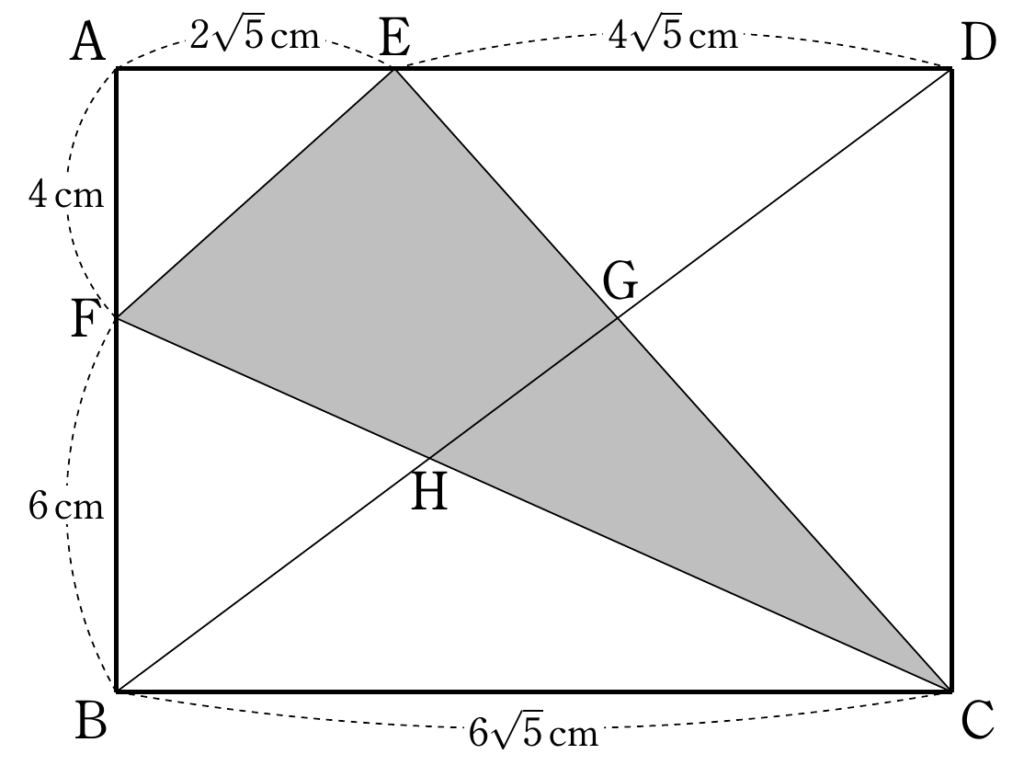
四角形BGEFの面積は △BCF（△CEF） の面積と一致することが、上記で証明されました。
この解き方の最大の肝は「計算の手数は、面積を求めるための１回しか使っていない」ことです。
私が平面図形を好きになったきっかけは、受験の時に解けなかった高校入試の問題を、できなかった未練を断つために解き直したことなのです。
だから、すでに終えた定期テスト、実力テスト、模擬試験、入学試験の問題を、全部じゃなくて良いから解き直してみることを強く勧めます。
「今までできなかったことが、できるようになってる！」「できなかったけど、あの時これさえ意識したら解けたな」などと自分で実感することが勉強の醍醐味でしたね。
勉強をやらされる、教えられるだけでは決して得ることのできない感覚です。
面積一致のからくり〔2021 愛媛県〕
今回は2021年に愛媛県公立高校で出題された問題の大問５の３を取り上げます。
愛媛県でも、新型コロナウイルスなどに対する配慮から出題範囲の削減は行われましたが、図形の問題には影響ありませんでした。
（三平方の定理も範囲に含まれています。）
長方形を折り返すだけであれば頻繁に見かけるのですが、唐突に線分BDを結んで交点Ｇをつくり、四角形BGEFを作っています。
一見すると少々面倒な計算問題ですが、解いてみると実は隠れた背景をもつ超良問であることがわかったのです。
目次〔2021 愛媛県 大問５の３のみ〕
……まずは普通に解いてみます。
……超良問と称した理由がここにあります！
↓ ここまでは２つの解き方で共通しています。
$\text{EF}=\text{BF}=6$ cmだから、△AEFにおいて三平方の定理より、
$\text{AE}=\sqrt{\text{EF}^2-\text{AF}^2}=2\sqrt{5}$ cm
△AEF∽△DCEより、
$\text{AE}:\text{DC}=\text{AF}:\text{DE}$
$2\sqrt{5}:10 = 4:\text{DE}$
$\text{DE}=4\sqrt{5}$ cm
普通の解き方
△BCG∽△DEGより、
$\text{BG}:\text{DG}=\text{BC}:\text{DE}=3:2$
よって、
△BEG $=\displaystyle{\frac35 △\text{BED}=12\sqrt{5}}\,\text{cm}^2$
また、
△BEF $=6\sqrt{5}\,\text{cm}^2 $
ゆえに、
四角形BGEF $=12\sqrt{5}+6\sqrt{5}=18\sqrt{5}\,\text{cm}^2 $
このくらいの計算問題であれば、対応できた受験生もいたかと思われます。
ただ、この $18\sqrt{5}$ という結果は、△BCF（△CEF）の面積と一致していることに着目します。
図形的性質を用いて解く
FG $/\!/$ BC であることを証明する。
$\text{AF}:\text{FB}$
$=\text{AF}:\text{FE}$ （折り返した図形の対応する辺 $\text{BF}=\text{EF}$より）
$=\text{DE}:\text{EC}$ （△AEF∽△DCEより）
$=\text{DE}:\text{BC}$ （ 折り返した図形の対応する辺 $\text{EC}=\text{BC}$より）
$=\text{DG}:\text{GB}$ （△BCG∽△DEGより）
よって、 FG $/\!/$ BC である。
BDとCFとの交点をHとすると、△BHF $=$ △CHGだから、
四角形BGEF
$=$ 四角形HGEF $+$ △BHF
$=$ 四角形HGEF $+$ △CHG
$=$ △CEF
よって、
四角形BGEF $= \displaystyle{\frac12\times 6\times 6\sqrt{5}=18\sqrt{5} \,\text{cm}^2 }$
四角形BGEFの面積は △BCF（△CEF） の面積と一致することが、上記で証明されました。
この解き方の最大の肝は「計算の手数は、面積を求めるための１回しか使っていない」ことです。
私が平面図形を好きになったきっかけは、受験の時に解けなかった高校入試の問題を、できなかった未練を断つために解き直したことなのです。
だから、すでに終えた定期テスト、実力テスト、模擬試験、入学試験の問題を、全部じゃなくて良いから解き直してみることを強く勧めます。
「今までできなかったことが、できるようになってる！」「できなかったけど、あの時これさえ意識したら解けたな」などと自分で実感することが勉強の醍醐味でしたね。
勉強をやらされる、教えられるだけでは決して得ることのできない感覚です。
共有: