正答率は22.5%だそうです。
直線 $\ell$ の切片についての条件に帰着させるのが難しいと感じる受験生が多そうですね。
ここでは、2通りの解き方を説明します。
① 直線 $\ell$ の式を $a$ を用いて表す(一般的な解き方)
② 線分比を用いて解く(スマートな解き方!)
解き方1: 直線lの式をaを用いて表す
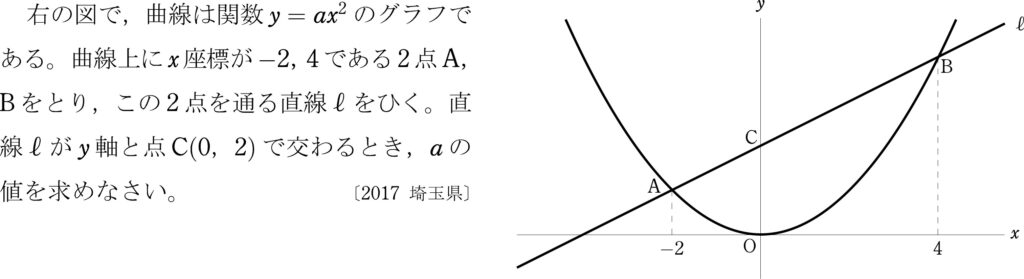
2点A、Bは関数 $y=ax^2$ のグラフ上にあるから、
A($-2$,$4a$)、B($4$,$16a$)
と表される。
直線 $\ell$ の傾きは、\(\displaystyle{\frac{16a-4a}{4-(-2)}=2a}\)
であるから、直線 $\ell$ の式は、$y=2ax+2$ とおける。
点Bは直線 $\ell$ 上の点であるから、B($4$,$8a+2$)と表される。
($x=4$ に対応する $y$ 座標は、直線 $\ell$ の式に $x=4$ を代入することで得られます。)
点Bの $y$ 座標について、
$16a=8a+2$
$\displaystyle{a=\frac{1}{4}}$
つまり、点Bの $y$ 座標を2通りに表して、方程式を解く方法です。
点Bが関数 $y=ax^2$ のグラフ上にあることを利用して、$y$ 座標を計算し、
さらに、点Bが直線 $\ell$ 上にあることを利用して、$y$ 座標を計算します。
そうすることで、点Bの $y$ 座標を2通りに表すことができ、その $y$ 座標が一致するように $a$ の値を定めれば良いことになります。
方程式に帰着するまでは、$a$ のまま解き進めることに慣れていないと難しく感じると思います。
解き方2: 線分比を用いて解く
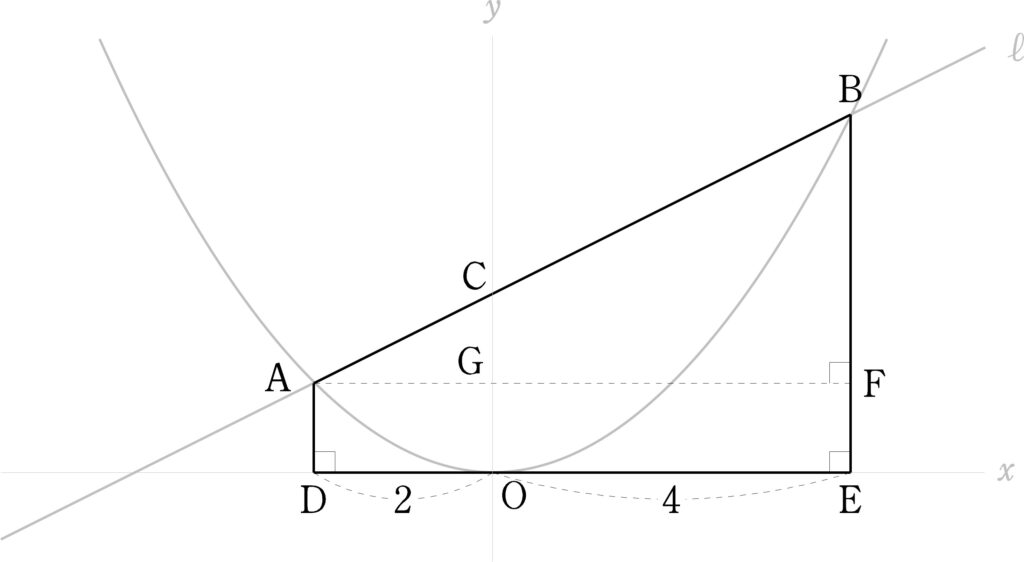
D $(-2,0)$、E $(4, 0)$ とする。点Aから直線BEに垂線をひき、その交点をFとする。直線AFと $y$ 軸との交点をGとする。
図1に示した太線の台形ADEBについて考える。
$x$ 座標が $-2$ から $4$ に変化すると $-2$ 倍になっているから、$y$ 座標は $(-2)^2$ 倍になるので、
AD $:$ BE $=1:4$
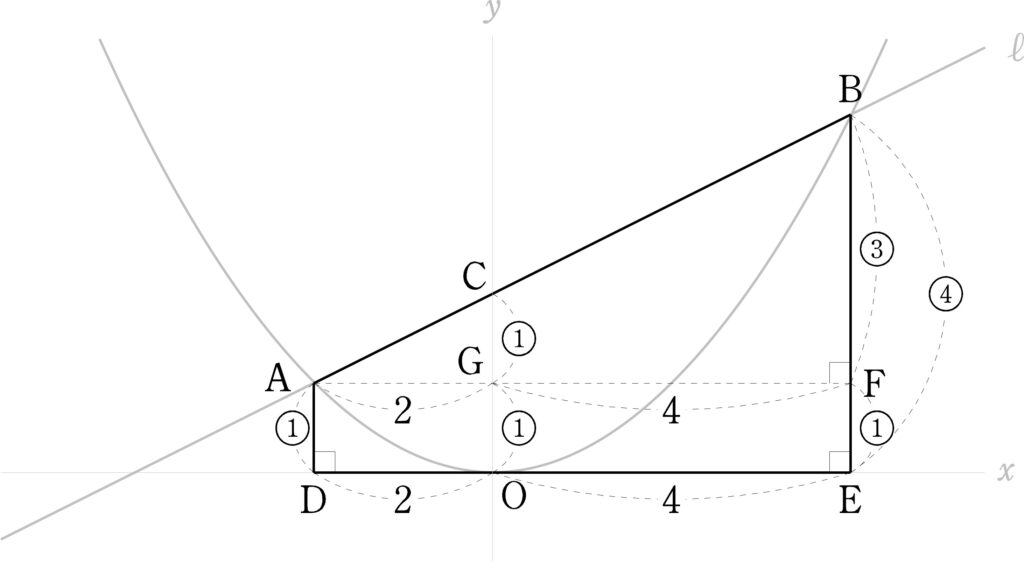
△AGC∽△AFBであるから、
GC $:$ FB $=$ AG $:$ AF $= 1:3$
よって、図2に丸文字で示した通りの線分比になる。
OC $:$ AD $ =2:1$より、
AD $=\displaystyle{\frac{1}{2}}$ AC $=1$
点Aは $y=ax^2$ のグラフ上の点であるから、
$1=a\times (-2)^2$
$a=\displaystyle{\frac14}$
 ↑ 図1
↑ 図1
 ↑ 図2
↑ 図2
こちらのほうが「スマートな解き方」と宣言しておきながら、きっちり説明すると解き方1よりも長くなってしまいます。
ただ、関数の式に代入する計算は、最後の1回しかしていないことが見て分かります。
このような図形的な性質を利用する方法は、理解には少し時間がかかりますが、計算の回数をできる限り減らすことができるのでオススメです☆彡
放物線の問題を線分比でスマートに解く〔2017 埼玉県〕
正答率は22.5%だそうです。
直線 $\ell$ の切片についての条件に帰着させるのが難しいと感じる受験生が多そうですね。
ここでは、2通りの解き方を説明します。
① 直線 $\ell$ の式を $a$ を用いて表す(一般的な解き方)
② 線分比を用いて解く(スマートな解き方!)
解き方1: 直線lの式をaを用いて表す
2点A、Bは関数 $y=ax^2$ のグラフ上にあるから、
A($-2$,$4a$)、B($4$,$16a$)
と表される。
直線 $\ell$ の傾きは、\(\displaystyle{\frac{16a-4a}{4-(-2)}=2a}\)
であるから、直線 $\ell$ の式は、$y=2ax+2$ とおける。
点Bは直線 $\ell$ 上の点であるから、B($4$,$8a+2$)と表される。
($x=4$ に対応する $y$ 座標は、直線 $\ell$ の式に $x=4$ を代入することで得られます。)
点Bの $y$ 座標について、
$16a=8a+2$
$\displaystyle{a=\frac{1}{4}}$
つまり、点Bの $y$ 座標を2通りに表して、方程式を解く方法です。
点Bが関数 $y=ax^2$ のグラフ上にあることを利用して、$y$ 座標を計算し、
さらに、点Bが直線 $\ell$ 上にあることを利用して、$y$ 座標を計算します。
そうすることで、点Bの $y$ 座標を2通りに表すことができ、その $y$ 座標が一致するように $a$ の値を定めれば良いことになります。
方程式に帰着するまでは、$a$ のまま解き進めることに慣れていないと難しく感じると思います。
解き方2: 線分比を用いて解く
D $(-2,0)$、E $(4, 0)$ とする。点Aから直線BEに垂線をひき、その交点をFとする。直線AFと $y$ 軸との交点をGとする。
図1に示した太線の台形ADEBについて考える。
$x$ 座標が $-2$ から $4$ に変化すると $-2$ 倍になっているから、$y$ 座標は $(-2)^2$ 倍になるので、
AD $:$ BE $=1:4$
△AGC∽△AFBであるから、
GC $:$ FB $=$ AG $:$ AF $= 1:3$
よって、図2に丸文字で示した通りの線分比になる。
OC $:$ AD $ =2:1$より、
AD $=\displaystyle{\frac{1}{2}}$ AC $=1$
点Aは $y=ax^2$ のグラフ上の点であるから、
$1=a\times (-2)^2$
$a=\displaystyle{\frac14}$
こちらのほうが「スマートな解き方」と宣言しておきながら、きっちり説明すると解き方1よりも長くなってしまいます。
ただ、関数の式に代入する計算は、最後の1回しかしていないことが見て分かります。
このような図形的な性質を利用する方法は、理解には少し時間がかかりますが、計算の回数をできる限り減らすことができるのでオススメです☆彡
共有:
オリジナル因数分解「分け分け法」拡張版
以前に投稿した因数分解のやり方を、一般の場合に公式化することに成功しました! 2021年9月1日の投稿では、高校入試問題を例に、中学生でもできる因数分解の応用問題を解説しました。内容につきましては、こ[…]
共有:
「正何角形?」問題は外角から攻める!
例題.次の条件を満たす正多角形は、正何角形か。 (1) 1つの内角の大きさが140°である。〔2021 青森県〕 (2) 1つの外角の大きさが40°である。〔2017 横浜学園高〕 (3) 1つの外角[…]
共有:
一次関数が苦手な子はここで詰まります
一次関数が苦手だという方は多いのではないのでしょうか。 苦手の程度は十人十色。彼ら彼女らの頭の中はざっとこんな感じでしょうか…。 そもそも一次関数って何?? なぜ増加量を求めるの? (ちょっと理解して[…]
共有:
実はたすき掛けを使わずにできる因数分解
次の式を因数分解しなさい。 $4a^4b^4-29a^2b^2+25$ 〔2018年 東京農業大学第一高 入試問題〕 東京農業大学第一高校は普通科で偏差値65の進学校です。(2021年8月「高校偏差値[…]
共有: