例題.次の条件を満たす正多角形は、正何角形か。
(1) 1つの内角の大きさが140°である。〔2021 青森県〕
(2) 1つの外角の大きさが40°である。〔2017 横浜学園高〕
(3) 1つの外角の大きさの9倍が、1つの内角の大きさと等しい。〔2021 京都府〕
上のような「正何角形か」の問題に苦手意識をもっている生徒は多いと思います。
「正n角形とおいて、1つの内角の大きさについてだから、まず内角の和を求めて…」のように考えられる生徒は、よく理解できていると思います。
では、↓ はすぐ理解できますでしょうか。
(1)と(2)は答えが同じ問題なのです。
正多角形において
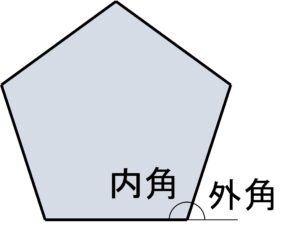
「1つの内角の大きさが140°である」ことと
「 1つの外角の大きさが40° である」ことは
全く同じ意味になります。
なぜなら、1つの内角と、それと隣り合う外角の和は180°だからです。
正多角形の1つの内角の大きさが140°ならば、1つの外角の大きさは
180°-140° = 40°
ですね。
外角から攻める!(本題)
「外角とは」を理解していただいたところで本題に入ります。
例題を解くのに必要な外角の公式は、この (☆) の公式だけです。
公式
$n\geqq 3$とする。$n$ 角形の外角の和は360°であるから、
正 $\boldsymbol{n}$ 角形の1つの外角の大きさは \(\displaystyle\boldsymbol{\frac{360°}{n}}\)
である。すなわち、
$\boldsymbol{n=360\div}$ (正多角形の1つの外角の大きさ) ……(☆)
上の (☆) の公式はかなり簡潔なので、人によっては暗算でもできるレベルになるのです。
直感的な理解が可能なうえ、
(参考:大日本図書「数学イメージ動画集」)
本質的には、よく知られた公式
内角の和 $= 180(n-2)°$
を使っていることと同じことなのです。
さきほどの例題を外角を使って解いてみます。
例題.次の条件を満たす正多角形は、正何角形か。
(1) 1つの内角の大きさが140°である。〔2021 青森県〕
(2) 1つの外角の大きさが40°である。〔2017 横浜学園高〕
(3) 1つの外角の大きさの9倍が、1つの内角の大きさと等しい。〔2021 京都府〕
解答例
(1)(2) 1つの外角の大きさが40°であるから、
$360°\div 40° = 9$ より、正九角形
(3) 1つの外角と、それと隣り合う内角の比が $1:9$であるから、1つの外角の大きさは
\(\displaystyle360°\times \frac{1}{1+9} = 36°\)
ゆえに、 $360°\div 36° = 10$ より、正十角形
…確かに、1つの外角の大きささえ求めに行けば勝ちであることが分かりますね。
さらに…何でもかんでも外角を使ってみる
「何でもかんでも」はさすがに言い過ぎですが、 内角の和に関する条件が与えられているときでさえも、外角を使って解いてみます。
例題.内角の和が720°である多角形は何角形か、答えなさい。〔2011 福島県〕
「正多角形」の話題からは少しそれていることにご注意ください。
上の例題は、$n$ 角形における次の事実を用いて解きます。
$\boldsymbol{n = } $(内角の和 + 360°)$\boldsymbol{\div 180}$
実はこの「360°」というのは外角の和を表し、
(内角の和) + (外角の和)
= (内角 + 外角) $n$ 個分の和
= $180n$°
となることが、上の事実が成り立つ理由となります。
 ↑ 内角と外角の和は180°でしたね。
↑ 内角と外角の和は180°でしたね。
解答例
$(720°+360°)\div 180 = 6$ より、六角形
外角を足しに行く発想は難しいですが、やはり外角の和が360°であることさえ覚えていれば解けてしまいます。
演習問題
最後に演習問題を掲載していますので、学習にご活用ください。
演習問題.次の問いに答えなさい。
(1) 正八角形の1つの外角の大きさを求めなさい。〔2020 埼玉県〕
(2) 正二十角形の1つの内角の大きさを求めなさい。〔2009 愛知教育大学附属高〕
(3) 内角の和が1800°である多角形は何角形か、答えなさい。〔2009 相愛高〕
(4) 1つの内角の大きさが140°である正多角形の辺の数を求めなさい。〔2002 親和女子高〕
(5) 1つの内角が、その外角より100°大きい正多角形がある。この多角形は正何角形か求めなさい。〔2013 弘前学院聖愛高〕
↓
↓
↓
↓
↓
↓
↓
↓
解答例
(1) $360°\div 8 = \boldsymbol{45°}$
(2) 正二十角形の1つの外角の大きさは
$360°\div 20 = 18°$
よって、1つの内角の大きさは
$180°-18° = \boldsymbol{162°}$
(3) $(1800° + 360°)\div 180 = 12$ より、十二角形
(4) 1つの外角の大きさは$180°-140° = 40°$であるから、
$360°\div 40° = 9$ より、求める数は 9
(多角形の辺の数は、「何角形」の数と同じです。)
(5) 1つの外角の大きさを $x$ とすると、$x+(x+100)=180°$
これを解くと、$x=40°$
ゆえに、$360°\div 40° = 9$ より、正九角形
「正何角形?」問題は外角から攻める!
例題.次の条件を満たす正多角形は、正何角形か。
(1) 1つの内角の大きさが140°である。〔2021 青森県〕
(2) 1つの外角の大きさが40°である。〔2017 横浜学園高〕
(3) 1つの外角の大きさの9倍が、1つの内角の大きさと等しい。〔2021 京都府〕
上のような「正何角形か」の問題に苦手意識をもっている生徒は多いと思います。
「正n角形とおいて、1つの内角の大きさについてだから、まず内角の和を求めて…」のように考えられる生徒は、よく理解できていると思います。
では、↓ はすぐ理解できますでしょうか。
(1)と(2)は答えが同じ問題なのです。
正多角形において
「1つの内角の大きさが140°である」ことと
「 1つの外角の大きさが40° である」ことは
全く同じ意味になります。
なぜなら、1つの内角と、それと隣り合う外角の和は180°だからです。
正多角形の1つの内角の大きさが140°ならば、1つの外角の大きさは
180°-140° = 40°
ですね。
外角から攻める!(本題)
「外角とは」を理解していただいたところで本題に入ります。
例題を解くのに必要な外角の公式は、この (☆) の公式だけです。
公式
$n\geqq 3$とする。$n$ 角形の外角の和は360°であるから、
正 $\boldsymbol{n}$ 角形の1つの外角の大きさは \(\displaystyle\boldsymbol{\frac{360°}{n}}\)
である。すなわち、
$\boldsymbol{n=360\div}$ (正多角形の1つの外角の大きさ) ……(☆)
上の (☆) の公式はかなり簡潔なので、人によっては暗算でもできるレベルになるのです。
直感的な理解が可能なうえ、
(参考:大日本図書「数学イメージ動画集」)
本質的には、よく知られた公式
内角の和 $= 180(n-2)°$
を使っていることと同じことなのです。
さきほどの例題を外角を使って解いてみます。
例題.次の条件を満たす正多角形は、正何角形か。
(1) 1つの内角の大きさが140°である。〔2021 青森県〕
(2) 1つの外角の大きさが40°である。〔2017 横浜学園高〕
(3) 1つの外角の大きさの9倍が、1つの内角の大きさと等しい。〔2021 京都府〕
解答例
(1)(2) 1つの外角の大きさが40°であるから、
$360°\div 40° = 9$ より、正九角形
(3) 1つの外角と、それと隣り合う内角の比が $1:9$であるから、1つの外角の大きさは
\(\displaystyle360°\times \frac{1}{1+9} = 36°\)
ゆえに、 $360°\div 36° = 10$ より、正十角形
…確かに、1つの外角の大きささえ求めに行けば勝ちであることが分かりますね。
さらに…何でもかんでも外角を使ってみる
「何でもかんでも」はさすがに言い過ぎですが、 内角の和に関する条件が与えられているときでさえも、外角を使って解いてみます。
例題.内角の和が720°である多角形は何角形か、答えなさい。〔2011 福島県〕
「正多角形」の話題からは少しそれていることにご注意ください。
上の例題は、$n$ 角形における次の事実を用いて解きます。
$\boldsymbol{n = } $(内角の和 + 360°)$\boldsymbol{\div 180}$
実はこの「360°」というのは外角の和を表し、
(内角の和) + (外角の和)
= (内角 + 外角) $n$ 個分の和
= $180n$°
となることが、上の事実が成り立つ理由となります。
解答例
$(720°+360°)\div 180 = 6$ より、六角形
外角を足しに行く発想は難しいですが、やはり外角の和が360°であることさえ覚えていれば解けてしまいます。
演習問題
最後に演習問題を掲載していますので、学習にご活用ください。
演習問題.次の問いに答えなさい。
(1) 正八角形の1つの外角の大きさを求めなさい。〔2020 埼玉県〕
(2) 正二十角形の1つの内角の大きさを求めなさい。〔2009 愛知教育大学附属高〕
(3) 内角の和が1800°である多角形は何角形か、答えなさい。〔2009 相愛高〕
(4) 1つの内角の大きさが140°である正多角形の辺の数を求めなさい。〔2002 親和女子高〕
(5) 1つの内角が、その外角より100°大きい正多角形がある。この多角形は正何角形か求めなさい。〔2013 弘前学院聖愛高〕
↓
↓
↓
↓
↓
↓
↓
↓
解答例
(1) $360°\div 8 = \boldsymbol{45°}$
(2) 正二十角形の1つの外角の大きさは
$360°\div 20 = 18°$
よって、1つの内角の大きさは
$180°-18° = \boldsymbol{162°}$
(3) $(1800° + 360°)\div 180 = 12$ より、十二角形
(4) 1つの外角の大きさは$180°-140° = 40°$であるから、
$360°\div 40° = 9$ より、求める数は 9
(多角形の辺の数は、「何角形」の数と同じです。)
(5) 1つの外角の大きさを $x$ とすると、$x+(x+100)=180°$
これを解くと、$x=40°$
ゆえに、$360°\div 40° = 9$ より、正九角形
共有:
放物線の問題を線分比でスマートに解く〔2017 埼玉県〕
正答率は22.5%だそうです。 直線 $\ell$ の切片についての条件に帰着させるのが難しいと感じる受験生が多そうですね。 ここでは、2通りの解き方を説明します。 ① 直線 $\ell$ の式を $[…]
共有:
オリジナル因数分解「分け分け法」拡張版
以前に投稿した因数分解のやり方を、一般の場合に公式化することに成功しました! 2021年9月1日の投稿では、高校入試問題を例に、中学生でもできる因数分解の応用問題を解説しました。内容につきましては、こ[…]
共有:
一次関数が苦手な子はここで詰まります
一次関数が苦手だという方は多いのではないのでしょうか。 苦手の程度は十人十色。彼ら彼女らの頭の中はざっとこんな感じでしょうか…。 そもそも一次関数って何?? なぜ増加量を求めるの? (ちょっと理解して[…]
共有:
実はたすき掛けを使わずにできる因数分解
次の式を因数分解しなさい。 $4a^4b^4-29a^2b^2+25$ 〔2018年 東京農業大学第一高 入試問題〕 東京農業大学第一高校は普通科で偏差値65の進学校です。(2021年8月「高校偏差値[…]
共有: