一次関数が苦手だという方は多いのではないのでしょうか。
苦手の程度は十人十色。
彼ら彼女らの頭の中はざっとこんな感じでしょうか…。
- そもそも一次関数って何??
- なぜ増加量を求めるの?
- (ちょっと理解してる生徒の場合)なぜxでもyでもなく、tを使うの?
今回は、数学が苦手な生徒にフォーカスを合わせて話したいと思います。
数学が苦手な生徒の場合、圧倒的に
「そもそも一次関数って何??」
な状態になっていることが多いです。
さらに一次関数以前の問題で、座標平面の基礎が抜けてしまっている子も一定数存在します。
ここで、一次関数を学ぶにあたって、つまづきやすい基本事項を下の画像に列挙しておきます。
(画像をクリックすると拡大表示されます。)
項目を一か所に詰めたので、少し見にくいかもしれませんが、
一次関数が苦手な人は、画像の①~⑬の基本事項をきちんと覚えているか、見直してみてください。
画像の①~⑬のような、一次関数$y=ax+b$ における
「$\boldsymbol{a}$ と $\boldsymbol{b}$ の数量的意味と図形的意味の紐付け」
さえできるようになれば、一次関数の単元の基礎は理解できます。
関数を教えていて意外だなと思ったことは、上の画像の①~④の内容(どちらが座標軸の正の方向か)が意識できていない生徒がいたことです。
右下がりの直線の式を求めるときに、傾きが負ではなく正になってしまう生徒が該当します。
一次関数のグラフの2通りのかき方
切片や傾きの性質を活かして、一次関数のグラフをかくことができれば、一次関数の最重要事項は理解しているといえます。
まず、例題を見てみましょう。
(画像をクリックすると、印刷可能なPDFが別タブで表示されます。)
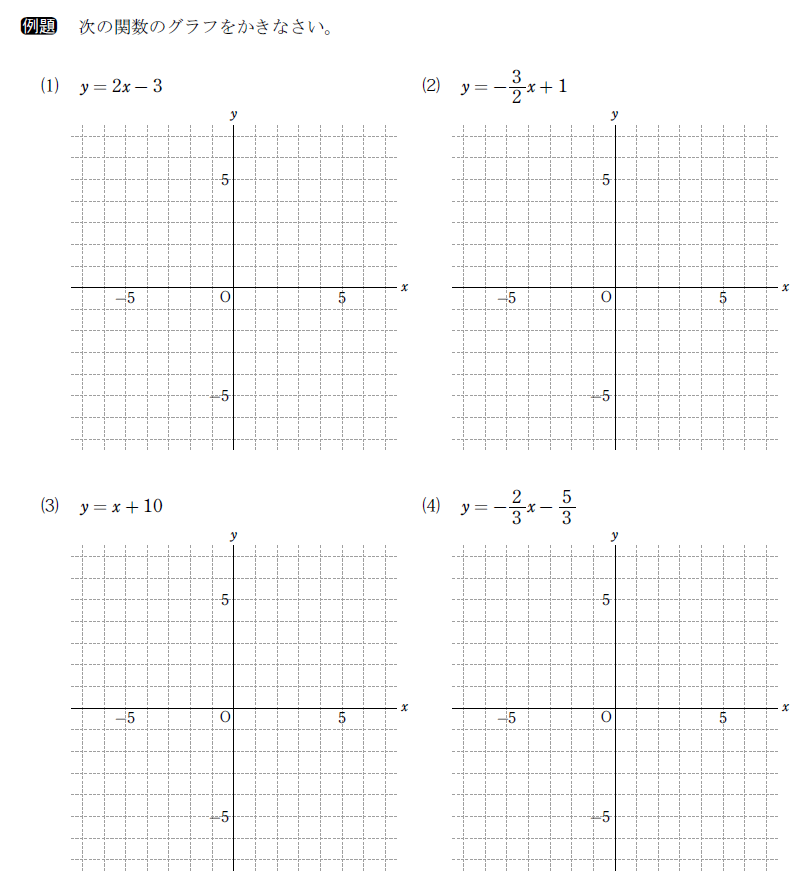
2通りのグラフのかき方を説明しますが、それぞれにデメリットがあります。
両方の方法を理解し、どの状況のときにどの方法でかくか覚えておいたほうが良いです。
ここでは、楽にグラフをかく方法のみ説明します。
x座標とy座標がともに整数になる点(格子点)を打って、それらをつなげる原始的な方法については省いています。
方法1.傾きと切片の性質を用いてかく(頻出)
(1)と(2)はこの方法でかけます。(解答例は一番下に掲載しています。)
(1)は、切片が $-3$ なので点 $(0,-3)$ を通ります。
傾きが2なので、$x$ の増加量が $1$ のときの $y$ の増加量が $2$ となるような直線をかけばOKです。
(右に1進むと上に2進む)
(2)は、切片が $1$ なので点 $(0,1)$ を通ります。
傾きが $-\tfrac32$ なので、 $x$ の増加量が $2$ のときの $y$ の増加量が $-3$ となるような直線をかけばOKです。
(右に2進むと下に3進む)
(3)は、切片が10なので、グラフとy軸との交点が座標平面からはみ出してしまうため、方法2を使います。
(4)は、切片が分数なので、中途半端な点を打つのを避けるために方法2を使います。
方法2.通る1点の座標と傾きを用いてかく
(3)と(4)はこの方法でかけます。
(3)は点 $(-7,3)$を通り、 $x$ の増加量が $1$ のときの $y$ の増加量が $1$ となるような直線をかけばOKです。
(4)は点 $(-7,3)$を通り、 $x$ の増加量が $3$ のときの $y$ の増加量が $-2$ となるような直線をかけばOKです。
((4)では、$x$ 座標、$y$ 座標がともに整数となるような点を基準とすれば良いです。)
したがって、例題の解答例は、以下のようになります。
(画像をクリックすると拡大表示されます。)
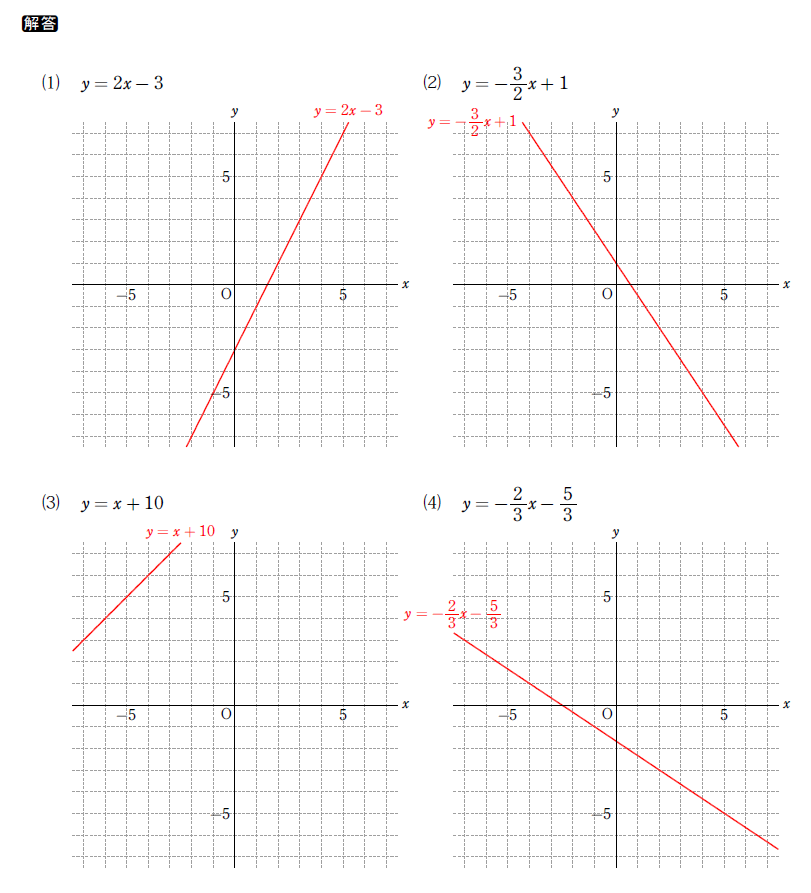
一次関数が苦手な子はここで詰まります
一次関数が苦手だという方は多いのではないのでしょうか。
苦手の程度は十人十色。
彼ら彼女らの頭の中はざっとこんな感じでしょうか…。
今回は、数学が苦手な生徒にフォーカスを合わせて話したいと思います。
数学が苦手な生徒の場合、圧倒的に
「そもそも一次関数って何??」
な状態になっていることが多いです。
さらに一次関数以前の問題で、座標平面の基礎が抜けてしまっている子も一定数存在します。
ここで、一次関数を学ぶにあたって、つまづきやすい基本事項を下の画像に列挙しておきます。
(画像をクリックすると拡大表示されます。)
項目を一か所に詰めたので、少し見にくいかもしれませんが、
一次関数が苦手な人は、画像の①~⑬の基本事項をきちんと覚えているか、見直してみてください。
画像の①~⑬のような、一次関数$y=ax+b$ における
「$\boldsymbol{a}$ と $\boldsymbol{b}$ の数量的意味と図形的意味の紐付け」
さえできるようになれば、一次関数の単元の基礎は理解できます。
関数を教えていて意外だなと思ったことは、上の画像の①~④の内容(どちらが座標軸の正の方向か)が意識できていない生徒がいたことです。
右下がりの直線の式を求めるときに、傾きが負ではなく正になってしまう生徒が該当します。
一次関数のグラフの2通りのかき方
切片や傾きの性質を活かして、一次関数のグラフをかくことができれば、一次関数の最重要事項は理解しているといえます。
まず、例題を見てみましょう。
(画像をクリックすると、印刷可能なPDFが別タブで表示されます。)
2通りのグラフのかき方を説明しますが、それぞれにデメリットがあります。
両方の方法を理解し、どの状況のときにどの方法でかくか覚えておいたほうが良いです。
ここでは、楽にグラフをかく方法のみ説明します。
x座標とy座標がともに整数になる点(格子点)を打って、それらをつなげる原始的な方法については省いています。
方法1.傾きと切片の性質を用いてかく(頻出)
(1)と(2)はこの方法でかけます。(解答例は一番下に掲載しています。)
(1)は、切片が $-3$ なので点 $(0,-3)$ を通ります。
傾きが2なので、$x$ の増加量が $1$ のときの $y$ の増加量が $2$ となるような直線をかけばOKです。
(右に1進むと上に2進む)
(2)は、切片が $1$ なので点 $(0,1)$ を通ります。
傾きが $-\tfrac32$ なので、 $x$ の増加量が $2$ のときの $y$ の増加量が $-3$ となるような直線をかけばOKです。
(右に2進むと下に3進む)
(3)は、切片が10なので、グラフとy軸との交点が座標平面からはみ出してしまうため、方法2を使います。
(4)は、切片が分数なので、中途半端な点を打つのを避けるために方法2を使います。
方法2.通る1点の座標と傾きを用いてかく
(3)と(4)はこの方法でかけます。
(3)は点 $(-7,3)$を通り、 $x$ の増加量が $1$ のときの $y$ の増加量が $1$ となるような直線をかけばOKです。
(4)は点 $(-7,3)$を通り、 $x$ の増加量が $3$ のときの $y$ の増加量が $-2$ となるような直線をかけばOKです。
((4)では、$x$ 座標、$y$ 座標がともに整数となるような点を基準とすれば良いです。)
したがって、例題の解答例は、以下のようになります。
(画像をクリックすると拡大表示されます。)
共有: