次の式を因数分解しなさい。
$4a^4b^4-29a^2b^2+25$
〔2018年 東京農業大学第一高 入試問題〕
東京農業大学第一高校は普通科で偏差値65の進学校です。
(2021年8月「高校偏差値.net」調べ)
数学の近年の入試問題を確認したところ、偏差値65にしては難度が高めの問題が出ているなあという印象です。
そのような問題を毎年コンスタントに出題できるほど、高校の先生方のレベルが高いと考えられます。
難関大学への合格率も上昇してきているそうです。
本問を解くための方針
高校数学の内容である「たすき掛け」という方法で因数分解をするのが一般的ですが、
今回は一般の中学生が解けるように、タイトルに記載した通りそれを使わないで解きます。
進学塾によっては、中学生でたすき掛けを教えるところもありますが、それは高校の先取り学習ができて、かつ、解答時間を短縮できるからです。
たすき掛けは中学校の学習指導要領から逸脱しているため、高校入試問題の大半はたすき掛けを使わなくても良いように工夫されています。
ここで再び $\boldsymbol{4a^4b^4-29a^2b^2+25}$ という式について見てみましょう。
係数「4」も定数「25」も平方数ですね。
(平方数というのは、整数の2乗で表すことができる数のことです。)
平方数も目の付け所としては良いのですが、それよりも「29」という数字を食い入るように眺めていただくと…
「肉」を食べたくなりましたか?(笑)
高校受験生の方は、肉の誘惑に負けずスクロールを止めてもらって、この問題を解いてみてください。
分からなくても大丈夫です。
しばらく下にスクロールすると解答例が見えますので、ぜひ理解していただきたいと思います。
↓
↓
↓
↓
↓
↓
↓
↓
↓
たすき掛けを使わない方法
以下、解答例です。
このように、29をうまい具合に「分け分け」することによって、2乗-2乗の式が2つ仲良く表れる、というストーリーが生まれるのです(笑)
「分け分け法」とよびましょうか。
また、次のように29を分け分けしてもOKです。
前者では3行目に共通因数 $(a^2b^2-1)$ が現れ、後者では3行目に $(4a^2b^2-25)$ が現れる、という違いがあります。
ただ、得られる因数分解の結果は同じですね。
それは、どんな因数分解のやり方をしても結果が一つに決まるという因数分解の一意性が保証されているためです。
たすき掛けを使って解く場合(高校数学)
せっかくなので、たすき掛けを使って解いてみましょう。
解答例は以下のようになります。
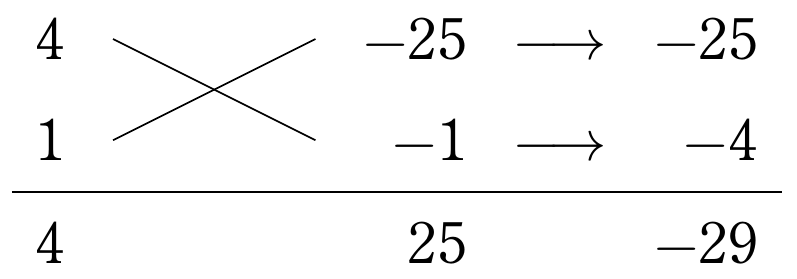
確かに、この方法で解けば時間短縮になりそうですね。
29を分ける発想は要らず、共通因数を見つける必要もなし、なので。
(補足)$\boldsymbol{a^2b^2=X}$ と置き換えると…
この置き換えを使うと、
$\ \ \ \ 4a^4b^4-29a^2b^2+25$
$=4X^2-29X+25$
となり(二次式)、式の眺めはグッと良くなります。
この先も 「分け分け法」で
$\ \ \ \ 4X^2-29X+25$
$=4X^2-4X-25X+25$
$=4X(X-1)-25(X-1)$
$=(X-1)(4X-25)$
$=(a^2b^2-1)(4a^2b^2-25)$
$=(ab+1)(ab-1)(2ab+5)(2ab-5)$
と因数分解できます。
(補足)$\boldsymbol{(2a^2b^2-5)^2}$ を使うと…
「4」と「25」が平方数であることから生まれた、すばらしい大胆な発想ですね!(自画自賛)
これを使うと
$\ \ \ \ 4a^4b^4-29a^2b^2+25$
$=(2a^2b^2-5)^2-(3ab)^2$
$=(2a^2b^2+3ab-5)(2a^2b^2-3ab-5)$
となって積の形に表せましたが、答えと一致しません。
それぞれの括弧の中の式は、さらに因数分解できるからです。
この先も、たすき掛けを使わなければ少々苦しい展開ですが、「分け分け法」で
$\ \ \ \ (2a^2b^2+3ab-5)(2a^2b^2-3ab-5) $
$=(2a^2b^2-2ab+5ab-5)(2a^2b^2+2ab-5ab-5)$
$=\{2ab(ab-1)+5(ab-1)\}\{2ab(ab+1)-5(ab+1)\}$
$=(ab-1)(2ab+5)(ab+1)(2ab-5)$
と因数分解できます。
ただ、高校数学ではこのように、2乗-2乗 の形を作り出して因数分解するパターンが存在するため、
発想として覚えておく価値は十分にあります。
結論:一般の中学生には難しい
29=4+25に分けることで、たすき掛けなし(「分け分け法」)で因数分解できました。
たすき掛けを知っている中学生にはかなり有利なのですが、一般の中学生が誘導なしで解くには難しいです。
ただ、難しいとはいっても、少し頭を捻れば解き方が思いつく問題なので、一般の中学生が解くことは可能です。
典型的な問題ばかりでなく、あまり類をみない新傾向の問題を入学試験に出題できる学校は、素晴らしいと思います。
入学試験の質によって「うちの学校は、その辺のありきたりな学校とは違うよ」という他校との差別化に貢献できるからです。
もちろん、学校を「入学試験の質」や「偏差値の高低」という狭い観点で見るべきではありませんが、
学問を深めることによって「試験問題に込められた意図を見る目」も養っていただきたいと思います。
最後に、実際の高校入試で出題されている因数分解の問題を載せておきます。
(たすき掛けを使わなくてもできるように工夫されています)
次の式を因数分解しなさい。
$(1)\ \ \ \ m^2+4mn+4n^2-36\ \ \ \ 〔2010\ 大阪星光学院高〕$
$(2)\ \ \ \ x^2+(2a-3b-6)x-6ab+18b\ \ \ \ 〔2016\ 開成高〕$
↓
↓ 解答例は下にあります。
↓
↓
↓
↓
↓
↓
↓
解答例(たすき掛けを使わない)
\begin{eqnarray*} (1)\ \ &&m^2+4mn+4n^2-36\\ &=&(m+2n)^2-6^2\\ &=&\boldsymbol{(m+2n+6)(m+2n-6)}\\[3mm] 別解\\ (1)\ \ &&m^2+4mn+4n^2-36\\ &=&m^2+(2n+6)m+(2n-6)m+(2n+6)(2n-6)\\ &=&m(m+2n+6)+(2n-6)(m+2n+6)\\ &=&\boldsymbol{(m+2n+6)(m+2n-6)}\\[1cm] (2)\ \ &&x^2+(2a-3b-6)x-6ab+18b\\ &=&x^2+(2a-6)x-3bx-6ab+18b\\ &=&x(x+2a-6)-3b(x+2a-6)\\ &=&\boldsymbol{(x-3b)(x+2a-6)}\\[3mm] 別解\\ (2)\ \ &&x^2+(2a-3b-6)x-6ab+18b\\ &=&(2x-6b)a+(-3x+18)b+x^2-6x\\ &=&2(x-3b)a-3(x-6)b+x(x-6)\\ &=&2(x-3b)a+(x-6)(x-3b)\\ &=&\boldsymbol{(x-3b)(x+2a-6)} \end{eqnarray*}


 (まだ評価がありません)
(まだ評価がありません) 0
0
Pingback: オリジナル因数分解「分け分け法」拡張版 – 学習塾DYB ブログ